I first knew I wanted to be a mathematician when Jenny and I started taking illegal shortcuts.
Jenny was my best friend in primary school. Every day we’d walk home from school together. Me, short and blond-haired with two pigtails sticking out right and left, her with a red ribbon in her thick, black hair. Both of us giggling and chatting about very important matters, like sticker collections or which Backstreet Boy was the cutest.
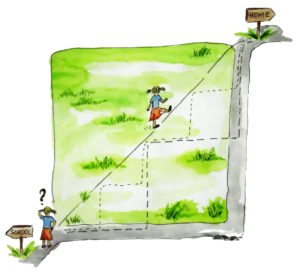
Our route always started at the school playground and ended at the tall cherry tree, which we climbed every autumn to pick the ripest cherries. Right in the middle of our path was a large, square lawn, always perfectly well-kept and the pride of its caretaker, the scary old lady who lived next door. We needed to get from one corner to the opposing corner, which left us with two choices: Either we could be good girls and stay on the path, which meant going straight, then turning left at a 90 degree angle, then going straight again. Or we could be bad girls and run diagonally through the grass, at risk of getting caught by the scary lady.
Jenny was always the more daring one. “C’mon,” she would say, “we’d be so much quicker and the old witch won’t catch us!” And many times we’d make a dash for it, often followed by the old lady’s voice shouting, “Next time, I’ll tell your parents!”
One quiet day during the summer holidays, I was walking home from the playground by myself. Jenny had gone to the Philippines to visit her mother’s family and even the old caretaker seemed to be on vacation. When I reached the critical corner, I pondered my route. Clearly the illegal route was fastest, but what if I zigzagged? I could stay on the path until halfway to the corner, make a 90 degree turn left to enter the grass, then turn right until I hit the path again and continue in the same way to the other end. Wouldn’t that take just as long as staying on the path? With measured steps I tried it out and proved my idea: there was no advantage. What if I zigzagged more, increasing the number of 90 degree turns? Same effect, it took me the same number of steps. But the more zigzags I added, the closer my path came to the diagonal short-cut, which was clearly shorter. How was that possible? My stepping experiments soon ran into problems, because the size of my sandals limited the number of zigzags, and I went home puzzled and confused.
Over dinner, I told my mum, a high school maths teacher, about my dilemma, carefully leaving out the details about the illegal lawn crossing. She smiled and explained that I was right that all my zigzag routes were equally long, but if I would have infinitely many zigzags, each of them infinitely tiny, then suddenly it would be the diagonal shortcut. The length of the path would then jump to that route’s shorter length. My pigtails wiggled as I shook my head in disbelief. In my head tiny, tiny zigzag lines were swirling and I was amazed how my mum could stay so calm and make sense of all of this.
This was the moment I realized that mathematics was not just about Susie buying four apples and Tom buying two apples and them happily eating their six apples. There seemed to be an entire universe out there, populated by infinitely small and infinitely large things, and mathematicians were somehow able to navigate through it. It was then that I decided I wanted to become part of that world and learn how to tame—or at least talk to—those curious, infinite beings.
[2016]
Angelika Manhart works as a biomathematician at New York University. She doesn’t wear pigtails anymore, but the infinite beings are regular guests in her office.